信息科学漫游 - The Hitchhiker's Guide to Information Science

The Hitchhiker’s Guide to Information Science

Intro

信息科学的世界广袤无垠，从抽象的数学原理到复杂的工程实践，各个领域交织融合，共同构筑起我们今日的数字文明。本指南旨在以笔者的个人视角，为您呈现一个独特的学习和探索路径，一同漫游于这片充满智慧与创新的“宇宙”之中。

本漫游并非 Wiki 或百科全书式的定义堆砌，也不追求面面俱到，而是尝试串联起这些学科的内在逻辑和演进脉络，探寻那些隐藏在学科间的幽微通道，理解它们是如何相互启发、互为表里，最终共同支撑起我们所见的数字世界。

在这里，我们主要关注以下学习和知识整合的要点：

解决知识零碎化问题： 现代学习很容易接触到大量信息，但这些信息往往是孤立的。通过“漫游”的方式，你可以主动将这些碎片串联起来，形成一个有机的知识网络。
深入理解而非堆砌细节： 很多时候我们会被细节淹没，忘记了学习某个知识的初衷和它在整个知识体系中的位置。“漫游”可以帮助你跳出细节，不被琐碎的细节淹没，而是尝试站在更高的维度审视知识。理解它在整个体系中的坐标，比单纯记住“怎么做”更重要。
关注“为什么学”： 第一性原理是学习的黄金准则，理解一个知识的“为什么”比单纯记住“是什么”和“怎么做”更为重要。它能激发学习兴趣，帮助你理解知识的本质和意义。
构建“全面概况”： 这就像是在脑海中绘制一幅知识地图。你知道这个领域的边界在哪里，主要的构成部分是什么，各个部分之间是如何联系的。这对于宏观把握和长远发展至关重要。
个性化的学习路径： “漫游”本身就带有一种自由探索的意味。你可以根据自己的兴趣和理解，规划自己的漫游路线，这比被动接受知识要有趣得多，也更符合认知规律。
输出是最好的输入： 将所学、所思写出来，是深度加工的过程。这一系列文章本身也是笔者“费曼学习法”的实践，愿这些文字能成为你思想的磨刀石。

Map

一个参考的知识联系图，这是主观化的，不构成任何学习顺序的参考：

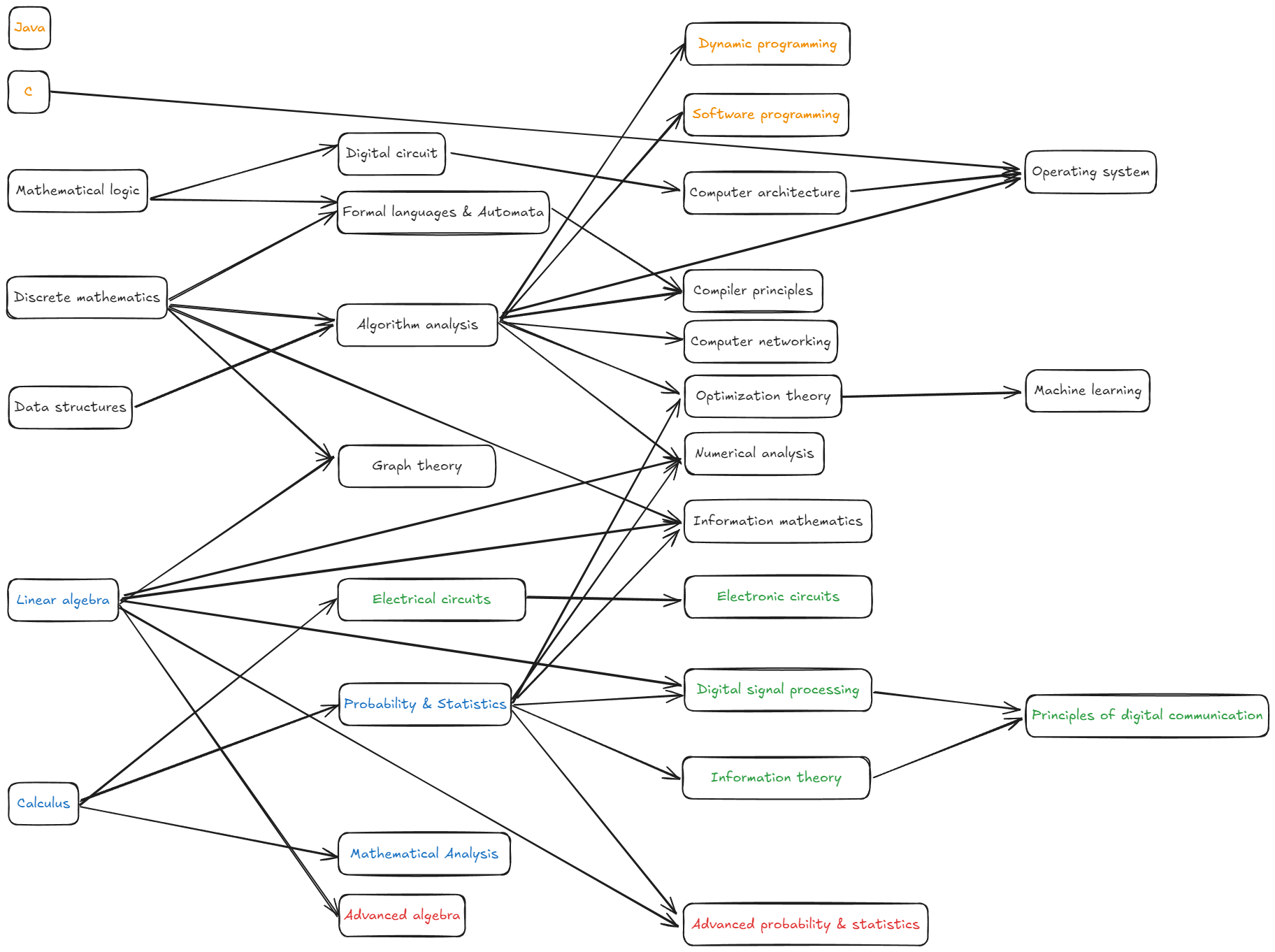
Wondering

本指南将主要分为以下几个篇章：

Mathematical Foundations：它是描述宇宙的通用语言。我们从这里出发，确立由数理基础构成的公理化世界观。
CS：深入计算机科学的核心。探讨如何用离散的逻辑捕捉信息，用算法驯服复杂度，以及如何构建从图灵机到操作系统的计算大厦。
EE：触及硬件的物理边界。理解信息如何载于电子与电磁波之上，在电路、信号与控制的协作下，打通物理世界与数字世界的接口。
Programming：从“道”落地为“术”。掌握 C 与 Java 等语言工具，理解网络基础设施，学习如何像工匠一样，将抽象的思想构建为坚实的工程现实。
Theory-Oriented：为更深层次的研究做准备。我们将潜入代数结构、随机过程与高维几何的深海，探索那些支撑前沿科技的抽象数学工具。

Science

Enjoy!

Mathematical Foundations

Linear algebra

线性代数漫游

在我们的学习旅程中，无论是算术中的加法交换律、结合律，还是代数中形如 $f(x)=kx$ (其中k为常数) 的正比例函数，都蕴含着一种重要的数学思想——线性 (linearity)。这种特性指的是，对于某个操作或映射 $f$：$f(x+y) = f(x)+f(y)$ 且 $f(kx) = kf(x)$。上述这些核心的线性性质——即“和的映射等于映射的和”以及“标量倍的映射等于映射的标量倍”——在数学和现实世界的诸多领域中都扮演着至关重要的角色。线性代数（Linear algebra）这门学科，正是系统地研究和处理与这些线性关系相关的代数结构和问题的理论体系。

为了系统地处理这些线性关系，我们引入了向量 (vector)。它可以表示具有大小和方向的物理量，或者更一般地，一组有序的数。当我们需要同时处理多个向量，或者描述向量之间的线性变换时，矩阵 (matrix) 就应运而生了。矩阵可以看作是向量的有序排列，也是表示线性方程组系数的紧凑形式，或线性组合的表达，也能够视作线性映射的直观身份。向量和矩阵（Vectors and matrices）是我们进行线性代数研究的基石，是我们将具体问题抽象化的重要工具。

事实上，线性代数的一个重要历史起源便是求解线性方程组（Solving linear equations）。在方程组中，每个未知数可以被理解为在某个维度上的分量或待定系数。通过将方程组的系数和常数项巧妙地组织成矩阵和向量的形式，我们发展出了多套使用矩阵运来系统、高效地求解方程组的方法。这套基于矩阵的理论和算法因其普适性和高效性而广受欢迎，能够处理从简单到极其复杂的各种线性方程组。

…（暂时未写，以后再写）

完成上面的内容，实际上你已经完全可以说自己学完了线性代数了，但也许你会想学更多，但后面的内容，将跳出人脑可以想象出的空间，步入用数学解释人脑不可想象的阶段了。因此线性代数发展到了一个更为抽象和理论化的阶段。它不再局限于我们直观可感的二维或三维几何空间，而是通过一组公理来定义向量空间（Vector space）。这种定义不依赖于几何直观，而是纯粹基于代数规则，强调的是元素之间运算所满足的普适性质。随着数学发展，人们发现这些线性性质不仅适用于实数（构成实数域 $\mathbb{R}$），也适用于复数（构成复数域 $\mathbb{C}$）等其他更广泛的代数结构（统称为域 (field)）。因此，我们可以讨论定义在实数域 $\mathbb{R}$ 上的向量空间（如 $\mathbb{R}^2, \mathbb{R}^3, \mathbb{R}^n$），也可以讨论定义在复数域 $\mathbb{C}$ 上的向量空间（如 $\mathbb{C}^2, \mathbb{C}^3, \mathbb{C}^n$）。尽管像 $\mathbb{C}^2$、$\mathbb{C}^3$ 这样的复向量空间在几何上不那么容易直接想象，但它们的代数结构、运算规则、子空间特性等都与我们熟悉的实向量空间类似，并且完全可以通过公理化的定义被严格地研究和理解。事实上，只要一组对象及在其上定义的“加法”和“标量乘法”运算满足向量空间的全部公理（例如，将一组来自特定域的数组织成列表形式，并恰当定义其运算），它们就能构成一个向量空间。正是这种高度的抽象性，使得线性代数能够将具有相似线性结构的问题统一起来进行一般性研究，展现出其强大的理论威力。

…（暂时未写，以后再写，下一个是有限维向量空间）

Calculus

Waiting for update…

Ordinary differential equations

Waiting for update…

Probability & Statistics

Waiting for update…

CS

Information mathematics

Waiting for update…

Numerical analysis

我们的计算机很强大，但它本质上只能做精确的、离散的加减法。可现实世界充满了连续的、无限的、无法求得精确解的数学问题（如解复杂的微分方程、计算积分）。数值分析，就是教计算机如何“近似”地解决这些”硬”数学问题的学科。它研究如何用有限的、离散的步骤，去逼近一个连续问题的真实解，并分析这个近似解的误差有多大。它让计算机能够模拟天气预报、设计飞机机翼、进行金融建模。这个宇宙，让我们的计算机从一个只能处理整数的”算盘”，变成了一个能解决复杂科学与工程问题的强大”数学家”。

Discrete mathematics

逻辑给了我们思考的规则，但世界并非都是连续平滑的。人是一个一个的，硬币有正反两面，计算机网络中的节点是一个一个的。离散数学，就是研究这些可数的、分离的对象的数学。它不像微积分那样研究平滑的曲线，而是研究点、线、集合、图这些看得见摸得着的”积木”。它教会我们如何计数（排列组合），如何研究关系（图论），如何描述状态的转换。如果说数理逻辑是思想的语法，那么离散数学就是思想的词汇表。它为我们提供了描述计算机世界里一切对象——从数据结构到网络拓扑——所需的最基本的数学语言。有了这些积木，我们才能开始搭建更宏伟的建筑。

Algorithm analysis

我们知道了机器“能”计算什么，但一个新问题出现了：它计算得“快”吗？对于同一个问题，比如“在一本电话簿里找一个名字”，我可以一页一页地翻，也可以每次都从中间翻开比较。两种方法都能找到，但效率却有天壤之别。算法分析（Algorithm analysis），就是为“效率”这件事建立起科学评判标准的学科。它真正关心的，是当问题的规模（比如电话簿的厚度）增长时，解决问题所需的时间和空间会如何随之增长。这个宇宙为“聪明”和“笨拙”的解法划定了界限，是软件工程的核心思想之一，更是区分“能用”程序和“好用”程序的关键。它最终的目标，是教我们如何从一名单纯的“代码实现者”，蜕变为一名洞察问题本质的“策略设计师”。

踏上这段旅程前，因为硬件的性能、环境的噪音都会掩盖思想本身，我们需要一种能够穿越时空、独立于具体机器之外的语言来描述运行时间。这意味着我们要学会“退后一步”，不再纠结于微小的常数差异，通过审视——当输入规模 n 趋向于无穷大时，代价是像平缓的对数曲线，还是像陡峭的指数高墙？这便是渐进记号（$O, \Omega, \Theta$）赋予我们的视角，它让我们忽略细枝末节只抓住那个决定性能生死的“主导项”。有了这把抽象的尺子，我们可以开始研习许多诸如分治策略（Divide-and-Conquer），概率分析（Probabilistic Analysis）等经典的战术，构建我们算法分析与设计的第一步。

基础夯实后，让我们踏入算法世界中最古老、也最迷人的竞技场：排序（Sorting）与搜索（Searching）。排序的本质，是驯服数据的混乱（熵减），它是计算机科学中大量算法的前奏。在这片战场上，我们见证了堆排序（Heapsort）如何巧妙地利用数据结构本身的特性来维持秩序，也惊叹于快速排序（Quicksort）在分治策略驱动下的雷霆速度与工程实用性。更重要的是，这里矗立着一道理论的壁垒——我们证明了任何基于比较的排序其效率极限都无法超越 $\Omega(n \lg n)$。但思维的魅力正在于突破边界，通过不再单纯依赖比较，而是利用数据本身的特征（如计数或桶），线性时间排序奇迹般地穿越了这堵高墙。而排序往往不是终点，当我们不需要全盘有序，只需精准定位混乱数据中的某一位（例如中位数）时，顺序统计量（Order statistics）展示了如何在不进行完全排序的情况下，以线性的代价完成这种外科手术式的精准搜索。

…未完待续 Waiting for update… 这部分篇章会很快更新… Will update soon…

Formal languages & Automata

我们有了逻辑、积木和度量衡，可以开始思考一个终极问题：能否建造一台能自动进行思考的机器？这台机器需要能理解一套严格的语言（形式语言），并根据规则自动执行操作。这就是”自动机”的诞生。从最简单的、只能识别特定模式的”有限自动机”（就像一个自动售货机），到更强大的、能处理嵌套结构的”下推自动机”，再到图灵提出的、理论上能模拟一切计算过程的终极机器——图灵机。这个宇宙探索的不是用什么物理材料造机器，而是在纯粹的数学和逻辑层面上，定义了”什么是计算？”、”什么是可计算的？”。它为计算机设定了理论的边界，是一切计算设备最原始的、抽象的祖先。

Mathematical logic

在一切开始之前，计算机科学世界一片混沌。我们如何确保我们的思考是”正确”的？一句断言，如何判定其为真或为假？如果我说”所有鸟都会飞”，你举出一只企鹅，就能驳斥我。这个简单的”举反例”过程，背后隐藏着严谨的规则。数理逻辑，就是为我们的思想和推理过程制定交通法规的学科。它定义了”与”、”或”、”非”、”如果…那么…“这些最基本的思维连接词，并教会我们如何从一组已知为真的”公理”出发，通过滴水不漏的推理，推导出新的、同样为真的”定理”。它不是关于计算，而是关于可信的思考本身。所以，在我们建造任何能”思考”的机器之前，我们必须先为”思考”这件事本身，建立起一套不容置疑的、坚如磐石的规则。

Compiler principles

我们仍然需要用机器能懂的语言（指令集）来写程序，这太痛苦了。我们希望能用更接近人类自然语言的方式来表达思想（如 if x > 3 then ...）。如何将这种”高级语言”翻译成机器能懂的”低级语言”？这便是编译器的使命。编译器原理，就是研究如何建造这座语言之桥的学科。它涉及词法分析（把代码切成一个个单词）、语法分析（检查语法是否正确，并建成一棵”语法树”）、语义分析和代码优化，最终生成高效的机器码。编译器是程序员最重要的伙伴，它让我们能专注于逻辑本身，而将繁琐的”翻译”工作自动化。

Computer architecture

我们如何将电路这些”砖块”组织起来，盖成一座能执行复杂任务的”大厦”？这就是计算机体系结构要解决的问题。它定义了一台计算机的宏观蓝图和功能划分。最著名的冯·诺依曼体系结构规定，一台计算机应该由运算器、控制器、存储器、输入设备和输出设备五部分组成。它还定义了”指令集”——也就是我们能对这台机器下达的最基本命令的集合（如加法、移动数据等）。体系结构决定了一台计算机的性格：它的计算速度有多快？它能同时处理多少数据？它的内存有多大？它就像是为这台机器设计了一套骨架和神经系统，规定了各个部件如何协同工作，共同完成我们交给它的任务。

Operating system

操作系统漫游

从CPU再往上，我们建造的是智能机器，但现在的使用方式却像是数学家每天手动操作铅笔和尺。能不能让机器自己安排任务、处理文件、管理资源？如果人必须去运行程序，那它就还不够聪明。这正是我们要通过“机器的自律”来解决的问题，而实现这份自律的核心，便是操作系统（Operating Systems）。简言之，“操作系统 = 机器之上的‘程序管理程序’”，它的目标不是执行计算指令，更是要将计算变成一种高效、有序、安全的流程。畅想一下：一旦有了操作系统，一台机器上将能同时运行多个程序，用户不再需要编写直接操作硬件的“裸程序”，而是提交“任务脚本”给系统裁决和执行。操作系统将建立起完善的权限模型、实现任务的优先级调度、并对所有计算资源进行统一管理。如果说编程语言是人与机器之间第一层级的“翻译官”，将我们的高级逻辑翻译成机器指令，那么操作系统，就是这位翻译官之上的“总调度师与首席翻译”，它将我们运行多个复杂任务、共享数据、安全交互的宏观意图，翻译并调度成底层硬件和程序能够协调执行的微观操作。所以，让我们启程，一同搭建这个“思想的机器”的灵魂，赋予它自己的“时间感知”、“资源意识”与“程序节奏”。

现在，让我们暂时忘却那些已经成型的操作系统产品，我们手中只有CPU和一堆硬件，我们将如何从零开始勾勒一个操作系统的总体设计草图呢？进入操作系统概述（OS general），我们的核心目标是什么？正如前文畅想的，我们希望一台机器能并发（Concurrency）执行多个程序，允许多个用户或任务同时使用，并且这些程序之间应能做到有效隔离，互不干扰。然而，在隔离的同时，我们也希望不同的程序能够高效且安全地共享（Sharing）资源，例如共同访问同一份内存数据进行计算，或协同使用打印机等外设。为了提升易用性、安全性并屏蔽底层硬件的复杂性，我们还需要实现虚拟化（Virtualization）。这意味着操作系统需要将物理CPU虚拟成多个逻辑CPU给不同程序使用，将物理内存虚拟成各自独立的地址空间，将磁盘抽象成文件系统等等，让程序仿佛独占整个机器。最后，我们还期望操作系统能够异步（Asynchronous Operations）地处理各种事件和I/O操作，例如当一个程序等待磁盘读取时，CPU不应空闲，而是能切换去执行其他就绪的任务，从而最大化系统吞吐率和响应速度。这就是我们设计操作系统的四大支柱理念。为了实现这些，我们必须精心设计任务调度的策略，制定清晰的权限管理规则，实现高效的I/O等待与唤醒机制，并明确操作系统的内核（Kernel）边界及其与用户程序的交互接口。至此，我们操作系统的初步设计蓝图便已成型。

为了让静态的程序代码真正“活”起来，在操作系统中并发地运行这样就能得到进程和线程（Process and threads）的概念。进程（Process）可以被看作是程序的一次执行实例，它拥有自己独立的内存空间、数据、以及一系列系统资源。它使得原本静止在磁盘上的程序代码，能够在CPU上动态地执行和推进。更进一步，为了在一个进程内部实现更细粒度的并发，从而充分利用CPU资源或处理并行任务，例如一个文字处理器程序可以同时进行用户输入响应、后台拼写检查和自动保存，我们引入了线程（Thread）的概念。线程是进程内部的一个执行单元，一个进程可以包含多个线程，它们共享进程的资源，但各自拥有独立的执行栈和程序计数器。然而，并发的引入并非没有代价，它也带来了新的挑战。不恰当的调度可能导致某些进程或线程“饿死”，永远得不到执行机会；对共享资源的无序访问则可能导致数据损坏或不一致；更严重的是，多个进程或线程在争夺资源时可能陷入死锁（Deadlock）——每个参与者都在等待对方释放资源，导致所有相关任务都无法继续执行。为了应对这些问题，操作系统必须提供强大的同步（Synchronization）与互斥（Mutual Exclusion）机制。我们需要运用诸如信号量（Semaphores）、互斥锁（Mutexes）等工具来精细地控制对共享资源的访问，确保操作的原子性和一致性。同时，我们也会探讨如何通过类似银行家算法（Banker’s Algorithm）等策略来预防或检测并解除死锁，从而构建一个稳定、高效的进程与线程管理子系统。这正是我们操作系统需要精心调度的核心任务之一。

随着程序在并发世界中动态运转，操作系统还必须扮演好“空间管家”的角色，即高效地管理和组织程序在内存中的“居所”。这就是内存管理（Memory Management）的核心任务。它不仅仅是简单地分配内存，更要确保进程间的隔离与保护，并尽可能高效地利用有限的物理资源。为此，操作系统通过一系列精巧的软硬件机制，引入了诸如分页（Paging）和分段（Segmentation）等关键技术，为每个进程营造出独立的虚拟地址空间。再配合各种页面置换算法，操作系统能够在物理内存不足时智能地进行数据腾挪，实现高效的空间复用。可以说，优秀的内存管理策略，与CPU调度策略一样，是支撑现代操作系统高效、稳定运行的关键所在。

我们的操作系统在管理程序的动态执行和内存空间方面已初具规模。但还有一个关键问题：数据如何才能超越程序的生命周期和机器的开关状态而被长久保存？日益增长的数据量和用户对便捷访问这些数据的渴望，迫使我们为操作系统增加文件系统（File System）模块。这正是我们日常操作的“文件”和“文件夹”得以存在的基石，其便利性不言而喻。文件系统通过引入诸如目录树的组织结构以及像索引分配这样的物理存储管理方法，使得海量数据能够在操作系统的统一管理下，被有条不紊地组织、高效地存取，并稳定地为用户提供服务，同时也确保了宝贵的存储空间得到充分利用。

至此，我们的操作系统已经能够调度CPU、管理内存、并组织持久化的文件。但若不能与外部世界有效沟通，其价值将大打折扣。无论是接收用户的键盘鼠标输入，将结果显示在屏幕上，还是通过网络与远端服务器交换数据，亦或是读写磁盘上的文件，都离不开与各种输入输出设备（I/O Devices）的交互。因此，一个功能完备的操作系统必须包含强大的输入输出系统（I/O System）。这个系统的核心目标是提供一个统一、高效、且对上层应用友好的接口来管理形形色色的外部设备。它通过实现设备独立性，使得应用程序可以用相似的方式操作不同的设备，而无需关心其物理特性和具体驱动细节。为了弥合高速CPU与通常较慢的I/O设备之间的速度鸿沟，并提高数据传输效率，I/O系统广泛采用了缓冲技术（Buffering），如在用户空间和内核空间设立缓冲区。

以CPU为核心，辅以我们精心设计的操作系统对其内存、存储设备和各类输入输出端口的有效管理，一个基础的、能够自主运行和处理任务的计算机系统模型已经初步呈现在我们面前。它不再是冰冷的硬件堆砌，而是拥有了“时间感知”（进程调度）、“空间意识”（内存管理）、“持久记忆”（文件系统）和“感官触角”（I/O系统）的智能实体。可以说，我们已经搭建起了现代计算机的骨架。然而，这仅仅是一个开始。正如任何伟大的工程一样，我们的操作系统还有广阔的优化空间和诸多高级特性等待探索，以应对日益复杂的应用场景和不断提升的性能、安全需求。

…未完待续未来将引入：

死锁（Deadlocks） 虚拟化和云（Virtualization and cloud） 多处理机系统（Mutiprocessor system） 安全性（Security）

Waiting for update…

Digital circuit

一切都还停留在纸和笔的抽象世界，我们要将这些思想赋予物理的形态。如何用现实世界的物质来代表逻辑上的”真”与”假”？我们决定用”高电平”和”低电平”这两个状态来对应。数字电路，就是研究如何用开关（晶体管）来搭建逻辑门的艺术。用几个开关，我们可以搭出一个”与门”、一个”或门”、一个”非门”。再用这些逻辑门，我们就能搭出更复杂的”加法器”。再用加法器和其他组件，我们就能搭出能存储、计算的更复杂的模块。这个宇宙，是连接抽象逻辑世界和物理世界的桥梁，它将纸上的0和1，变成了硅片上真实流动的电流。

Machine learning

至此，我们所有的程序和系统，其行为模式都是由人类明确编程和设计的。机器只是在忠实地执行我们写下的每一条规则。但我们能否让机器自己从数据中”学习”出规则来？比如，给它看成千上万张猫的照片，让它自己”悟”出什么是猫，而不是我们去编程定义”猫是有胡须、有尖耳朵的动物”。这就是机器学习的革命。它让机器从一个听话的”仆人”，变成了一个能够自主学习的”学徒”。通过各种算法模型（如神经网络），机器可以在海量数据中发现我们人类自己都未曾察觉的模式。这个宇宙，正在从根本上改变我们与机器的交互方式，开启了通往真正”人工智能”的大门。

EE

Circuits

If Computer Science constructs the soul of the digital world, Circuits forge its body. Whether it is the chips bearing logic or the networks transmitting signals, everything ultimately boils down to the dance of electrons within physical media. However, through the lens of circuit analysis, we do not grapple directly with complex Maxwell’s equations or microscopic particle physics. Relying on the classic circuit framework, we perform a grand engineering abstraction: the establishment of the Lumped Circuit Model. In this model, intricate electromagnetic field effects are “lumped” into Idealized Elements; spatial wave propagation is ignored in favor of focusing on Voltage and Current at terminals. This abstraction empowers us to use Fundamental Circuit Laws to describe the transfer of energy and the processing of information via elegant algebraic and differential equations. Circuit theory is the cornerstone connecting physical laws to engineering implementation, teaching us how to tame electrons to flow exactly as we desire.

To establish this abstract model, we first step into a pure realm where time stands still—Direct Current Circuits (DC Circuits). To define the language, charges are no longer chaotic clouds of microscopic physics but are quantified into precise Current and Voltage, representing the rate of flow and the potential to push. To define the building blocks, we introduce the Resistor, which constrains energy dissipation through the purest proportionality ($V=IR$), and the independent and controlled Sources, continuously injecting order into the system. Finally, to define the constitution, these elements do not act randomly; when interwoven into a network, they strictly adhere to Kirchhoff’s Laws. Here, KCL guards the conservation of charge, while KVL defends the closed loop of energy. These two pillars transform physical topology into elegant systems of linear equations ($Ax=b$), empowering us to pierce through every corner via systematic methodologies and even condense the entire complex network into simple equivalents.

Yet, a universe frozen in time is lifeless. To capture the rhythm of reality, we must set these variables in motion, entering the dynamic realm of Alternating Current (AC Circuits). Here, the stage expands with the introduction of Inductors and Capacitors. Unlike the resistor, these are storage elements, capturing energy in magnetic and electric fields, thereby transforming simple algebraic constraints into dynamic differential equations. The complexity seems daunting, but we find salvation in the Phasor Method. By leveraging Euler’s identity, we map time-domain sinusoids into the complex plane, converting difficult calculus back into elegant complex algebra. In this domain, resistance evolves into Impedance, unifying resistors, inductors, and capacitors under a generalized Ohm’s Law. This new perspective unveils phenomena invisible in the DC world: the rhythmic exchange of energy known as Resonance, the wireless transfer of power via Magnetic Coupling and Transformers, and the industrial Polyphase Circuits. Ultimately, we ascend to the perspective of Fourier Transform, realizing that any complex signal is merely a superposition of sinusoids, allowing us to perceive the world not just as a sequence of moments, but as a spectrum of frequencies.

However, the universe is rarely in a state of eternal equilibrium; it is defined by change. When a switch toggles or a fault occurs, shattering the peace of steady-state, the circuit does not jump instantly to a new state but evolves through a Transient Response. Governed by the inertia of energy stored in inductors and capacitors, we witness the Natural Response as energy decays and the Step Response as the system tracks a sudden input. While simple first-order circuits yield to basic differential equations, complex networks entangle us in a web of intractable high-order calculus. To transcend this barrier, we invoke the Laplace Transform, which lifts us from the time domain into the generalized s-Domain (Complex Frequency Domain). Here, differentiation becomes simple multiplication by $s$, reducing the most formidable differential equations into algebraic Transfer Functions. Through the geography of Poles and Zeros in the s-plane, we gain a global insight into the system, predicting stability and dynamic behavior without ever solving a differential equation directly, completing our mastery over both the moment of change and the eternity of stability.

Even with these profound tools, analyzing every node within a massive interconnected system remains computationally paralyzing. True engineering is often more about the flow of information or power from point A to point B, leading to an architectural abstraction: the Two-Port Network. We encapsulate the circuit’s internal complexities within a “Black Box,” leaving only an input port to receive signals and an output port to deliver them. To characterize this box, we inject linear algebra. By defining parameter matrices, we compress the entire network’s behavior into an elegant set of algebraic equations, which transforms complex circuits into modular building blocks. The true miracle manifests in Cascading. When we chain amplifiers, filters, or transmission lines end-to-end, we simply multiply their transmission matrices. This paradigm shift, from calculating individual components to manipulating matrix modules, elevates circuit theory to the macroscopic height of System Engineering, bridging the raw flow of electrons to high-level system design.

However, at the extreme boundaries of scale and speed, our foundational abstraction has a fatal limitation. When frequencies soar into the microwave spectrum or physical wires stretch across continents, the fundamental assumption of the Lumped Circuit Model inevitably collapses. A wire is no longer a perfect, instantaneous conduit; it exhibits a continuum of distributed resistance, inductance, and capacitance. To address this physical reality, we must transition to Distributed Parameter Circuits, introducing the framework of the Uniform Transmission Line. By slicing the wire into infinitesimal segments and applying our laws to space and time simultaneously, we derive the Transmission Line Equations (Telegrapher’s Equations). In this realm, voltage and current cease to be mere scalar states at a node but transform into waves traveling through space. This perspective reveals phenomena: the finite propagation delay, the Reflection of energy from mismatched loads, and the establishment of Characteristic Impedance. The essence of this model lies in enabling wave management through Impedance Matching, ensuring maximum power transfer without destructive echoes.

Ultimately, having mastered these fundamental models, we stand on the precipice of a new continent. By merely adding two letters, we move from the traditional Electric Circuit to the modern Electronic Circuit (Microelectronic circuits), shifting focus from power to computation. We do not need to plunge into the quantum physics of semiconductors; our macroscopic framework is sufficient. At the heart of this revolution lies the Operational Amplifier (Op-Amp). By treating this complex integrated block as a pure circuit model, the Op-Amp is governed by the elegant constraints and stabilized by negative feedback, which enables active mathematics: addition, integration, differentiation, using nothing but resistors and capacitors. From these building blocks, we can also build crucial models like the Digital-to-Analog Converter (DAC), forging the physical bridge between the continuous analog reality and the discrete digital mind. Beyond that, from filters and oscillators to DC-DC converters and ADCs—all are variations on these themes. The mathematical and physical scaffolding of the circuit world is erected; the electrons have been tamed. Now, they are ready to compute.

End - Circuits

Communication principles

Not yet learned…

Waiting for update…

Digital signal processing

We inhabit a universe constructed of continuous physical variables: the vibration of vocal cords merging into speech, the reflection of light waves forming images, and radio waves carrying communication. These physical quantities that vary with time are Signals; and the entities capable of responding to, transforming, and processing these signals constitute Systems. The world of Continuous-time is a mathematical mirror of physical reality. However, to leverage the immense computational power of modern machines, we must traverse the bridge of the Sampling Theorem, slicing the smooth analog world into discrete sequences to enter the realm of Discrete-time. Signal processing is more than mere digitization; it is a cognitive ascension. We leap from the intuitive Time Domain into the profound Frequency Domain and even the Complex Frequency Domain. Through Fourier analysis, convolution, and from the Z-Transform to the Fast Fourier Transform (FFT), these mathematical instruments serve as the interpreter between the physical world and the digital brain. They grant us a “mathematical scalpel,” enabling us to precisely filter noise, extract features, compress data, and even reconstruct the reality we seek to perceive.

Before diving into the intricacies of digital algorithms, we must first establish our camp on the high ground of mathematical abstraction, investigating the fundamental laws of interaction between general signals and general systems: Signals are mathematically functions dependent on one or more independent variables that carry information and patterns, which can be decomposed into fundamental building blocks—Unit Impulses and Complex Exponentials; and Systems, which act as transformations mapping input signals to output signals. Signals may be periodic or aperiodic, possessing energy or power; systems may possess many properties, where the most critical are Linearity and Time-Invariance. Linearity implies that the system satisfies the principle of superposition, while Time-Invariance ensures that the system’s behavioral characteristics do not change as time shifts. When a system possesses both, it is termed a Linear Time-Invariant (LTI) System, which serves as the golden key to the complex world of signal processing.

Since any signal can be mathematically decomposed into a series of scaled and shifted unit impulses (in the discrete realm) or continuous impulse functions (in the continuous realm), the LTI properties allow us to treat the system’s response to any complex input as the weighted superposition of its responses to these individual impulses. This profound logical deduction leads to the most fundamental operation in time-domain analysis: Convolution (manifesting as the Convolution Sum in Discrete-time LTI Systems, and the Convolution Integral in Continuous-time LTI Systems). This reveals a startling fact: we need only capture the system’s response to the simplest “unit impulse”—the Impulse Response—to completely characterize and predict the system’s behavior for any input signal in the universe via convolution.

While convolution perfectly characterizes time-domain behavior, we yearn for a more efficient perspective, turning our gaze to the “Eigenfunctions” of LTI systems: Complex Exponentials. For Periodic Signals, this shift in perspective gives birth to the Fourier Series (FS). Whether manifested as an infinite series in continuous time or a finite sum in discrete time, the essence remains identical: decomposing a complex periodic signal into a linear combination of Harmonically Related complex exponentials. This is more than a mathematical reconstruction; it marks our formal entry into the Frequency Domain. Through the Fourier Series, we cease to focus on the signal’s value at a specific instant and instead focus on the frequency components it contains.

However, most signals in the real world—a burst of speech or a sudden crash—are not repetitive. To capture the essence of these Aperiodic Signals, we push the concept of periodicity to its limit, imagining the period stretching to infinity. Under this limiting perspective, the discrete harmonic lines densify and ultimately merge into a continuum, giving birth to the Continuous-Time Fourier Transform (CTFT). This is not merely a mathematical extension but a dimensional leap—we completely map signals from the time domain into a new space based on Frequency. In this new realm, operations that are excruciatingly complex in the time domain, such as convolution, miraculously simplify into algebraic multiplication. This analytical approach centered on spectral magnitude and phase, grants us the insight to instantly grasp the underlying simplicity within complex signals, rendering effortless what was once intractable.

When we cast the transformative gaze upon discrete aperiodic sequences, the Discrete-Time Fourier Transform (DTFT) emerges. Since discrete time is always an integer, shifting the frequency $\omega$ by $2\pi$ merely completes a full circle on the complex plane, returning to the origin (i.e., $e^{j(\omega+2\pi)n} \equiv e^{j\omega n}$), revealing a spectacle unique to the discrete world: the Periodicity of the spectrum. This seemingly minor characteristic places the final piece of the puzzle, compelling us to look back at the earlier series and transforms to behold the unified Duality across the four forms of Fourier analysis: Discretization in one domain inevitably leads to periodization in the other, and vice versa. This perfect symmetry constitutes the most harmonious mathematical beauty in signal processing, linking all seemingly independent tools into a complete theoretical loop.

Armed with the powerful mathematical tool of the Fourier Transform, we are no longer content with merely calculating results; we seek to probe the physical significance behind them. By separating the complex spectrum into Magnitude and Phase, we gain a novel perspective for dissecting systems: the magnitude response tells us how a system acts as a Filter, passing or suppressing energy at specific frequencies, while the phase response reveals the delay and distortion of the signal in time. This approach of Magnitude-Phase Separation not only gives rise to classic engineering analysis tools like Bode Plots but also brings us in touch with the deeper equilibrium between the time and frequency domains—as illustrated by the uncertainty principle, concentrating a signal in time inevitably leads to its expansion in frequency. At this point, we can not only compute signals but profoundly “comprehend” the character of systems.

Now, we traverse the most precipitous and magnificent bridge: the Sampling Theorem, which serves not only as the link between the continuous analog world and the discrete digital world but also as the climactic chapter that unifies Fourier analysis. Sampling is not merely “reading values”; mathematically, it is equivalent to “modulating” a continuous signal with an infinite Periodic Impulse Train. According to the convolution theorem, multiplication in the time domain corresponds to convolution in the frequency domain. This means the original signal’s spectrum is “shifted” and undergoes infinite periodic replication by the impulse train’s spectrum. This leads to the peril of Aliasing and the salvation of Nyquist: as long as the sampling frequency is sufficiently high, these replicated spectra will not overlap. Even more astoundingly, using an ideal low-pass filter, we can achieve perfect reconstruction of the original continuous waveform from discrete samples. This is not just an engineering triumph but a philosophical miracle: we discard infinite points in time, yet retain the complete reality.

Having mastered the secrets of spectral shifting (using convolution), we are empowered to construct Communication Systems. At their core lies Modulation—whether adjusting Amplitude (AM), Frequency (FM), or Phase (PM), the essence is fundamentally using sinusoids as carriers to “transport” low-frequency information signals onto high-frequency channels suitable for transmission. This precise control over spectral positioning enables Multiplexing, allowing countless signals to traverse the same wire or airspace simultaneously without interference such as Frequency Division Multiplexing (FDM), which not only demonstrates the engineering power of Fourier analysis but also serves as the prelude to the new profound domain.

However, the Fourier Transform faces a fundamental barrier: convergence. It struggles with signals that grow exponentially or systems that only begin at a specific instant. To break this, we introduce a convergence factor $e^{-\sigma t}$ to tame unruly growth, generalizing our perspective into the Laplace Transform. This is a dimensional leap from a single line, the $j\omega$ axis, to the vast s-plane. In this domain, we no longer just calculate; we see the system’s soul through its Poles and Zeros. By transforming intractable differential equations into simple algebra via the Transfer Function $H(s)$, Laplace grants us a global insight into stability and dynamics, allowing us to design the architecture of feedback and control systems with surgical precision.

In the discrete realm, we seek a counterpart to Laplace’s power. The Z-Transform serves this role, acting as the discrete bridge to the complex frequency domain. By mapping the s-plane onto the z-plane, where the unit circle embodies the frequencies we once explored via the DTFT, we gain the ability to algebraize the recursive logic of Difference Equations. The stability of a digital system is no longer a temporal mystery; it is inscribed in whether its poles reside within the protective boundary of the unit circle. This transform provides the blueprint for designing Digital Filters, enabling us to sculpt discrete sequences with the same mathematical elegance we applied to continuous waves.

Finally, all these mathematical tributaries—time, frequency, and complex domains—converge into the ocean of Digital Signal Processing (DSP). Here, the abstract $H(z)$ materializes into algorithmic reality: Digital Filters. Whether through the stability of FIR or the mimicking efficiency of IIR, we are no longer just observing signals; we are actively shaping them through difference equations. Coupled with the Fast Fourier Transform (FFT), which shatters the $O(N^2)$ barrier to unleash real-time spectral analysis, we gain the power to manipulate the fabric of reality—sound, image, and data, purely through the binary logic and computation. This is the summit where mathematics becomes engineering, and where a computer transcends its silicon nature to become a sensory organ of the world.

End - Digital signal processing

Information theory

How do we measure the essence of what we communicate? Does the statement “the sun will rise tomorrow” contain the same amount of “stuff” as “the winning lottery numbers are 12345”? Intuitively, no. Information Theory was the first to precisely measure this elusive concept of information using the language of mathematics. It reveals a profound truth: the amount of information is fundamentally determined by how much uncertainty it eliminates. An almost inevitable event carries an information content approaching zero, whereas a highly improbable miracle contains a massive amount of information. Beyond mere measurement, this discipline establishes the absolute boundaries of our digital universe. Information theory serves as the “law of conservation of energy” for the digital world, standing as the theoretical bedrock for all modern data compression, error correction, and communication technologies.

To mathematically capture this “uncertainty,” we must first step onto the bridge of Probability Theory. Our world is fundamentally stochastic; from the flipping of a coin to the static on a radio, chaos is the norm. To tame this randomness, mathematics introduced the Random Variable, a conceptual tool that maps unpredictable outcomes into measurable numbers, governed by a Probability Distribution that describes the entire landscape of likelihoods. However, traditional probability alone merely answers “how likely an event is.” To answer “how much information it carries,” Shannon defined the “surprise” of an event, i.e. its Self-Information, as a logarithmic function of its inverse probability ($I(x) = -\log_2 P(x)$). Why a logarithm? Because it perfectly satisfies human intuition: when two Independent events occur simultaneously, their probabilities multiply, but the total information they provide should naturally add up. Finally, by calculating the statistical average, or the Expected Value, of this self-information across the entire probability distribution, we successfully forge the key to unlock the ultimate metric of the digital universe.

Turning the key forged by expectation, we officially unlock the gates of Information Theory, confronting its most central concept: Information Entropy ($H$). If self-information measures the shock of a single event, Entropy measures the inherent, average uncertainty of an entire system—an Information Source. However, variables in our universe rarely exist in pure isolation. Imagine trying to guess the weather: if you are told the sky is overcast, your uncertainty about whether it will rain dramatically decreases. This remaining doubt, under the illumination of known evidence, is Conditional Entropy ($H(X

Y)$). The amount of uncertainty that was eliminated by this shared knowledge reveals a profound intersection known as Mutual Information ($I(X;Y)$), which answers the most critical question in communication: how much does observing a received signal actually tell me about the original message? However, to truly understand a flowing data stream, we must expand our view across time. A sequence of letters or weather patterns is rarely “memoryless”; the past profoundly influences the present. To capture this temporal Memory, we embrace the elegance of the Markov Chain, a model where the future depends solely on the current state. By acknowledging this, we discover that the true Entropy Rate of a source is often far lower than assuming all events are independent. This mathematical revelation exposes the immense “redundancy” hidden within human languages and digital signals, pointing straight toward the holy grail of information theory: Data Compression.

Driven by the discovery of this redundancy, we embark on the quest for Data Compression. The most primitive instinct is Fixed-Length Coding—assigning the same number of bits to every symbol, much like standard ASCII, entirely blind to the landscape of probability. To squeeze out this mathematical void, we must let probability dictate the structure, giving birth to Variable-Length Coding. By assigning the shortest bit strings to the most frequent occurrences and longer strings to rare anomalies, we drastically shrink the data’s footprint. The crown jewel is Huffman Coding, an algorithm that constructs an optimal binary tree from the bottom up based purely on statistical frequency. But can we compress infinitely? Absolutely not. Here, Shannon’s First Theorem (Source Coding Theorem) mercilessly decrees that for any Lossless Compression, the average code length can never drop below the source’s Entropy. We have perfectly squeezed out the statistical redundancy, hitting the absolute mathematical floor. But in the face of massive audio and video streams, hitting this entropy floor is still not enough. To break this boundary, we must make a dangerous but inevitable compromise.

To pierce through the absolute floor of entropy, we enter the realm of Lossy Compression. While Huffman coding squeezed out statistical redundancy, the multimedia streams of our world harbor massive spatial and temporal redundancy. Why transmit every pixel of a static sky across consecutive video frames? To exploit this, we introduce Predictive Coding. By using the known past or surrounding context to guess the present, we no longer transmit the raw data, but only the unpredictable “residual error.” As our prediction algorithms approach perfection, this residual error loses all recognizable structure, approaching the state of Maximum Entropy—pure, uncorrelated white noise. The closer our compressed data resembles total chaos, the higher our ultimate Coding Efficiency. When even this compressed chaos is too large for our networks, we must cross the final boundary: intentionally introducing distortion by exploiting the blind spots of human perception (such as discarding inaudible high frequencies). But how much can we distort before the soul of the message is destroyed? Shannon’s Third Theorem (Rate-Distortion Theorem) maps the precise, unyielding mathematical frontier between the minimum required bitrate (Rate) and the maximum acceptable degradation (Distortion). It proves that “loss” is never arbitrary destruction, but a deeply calculated optimization, allowing us to squeeze majestic symphonies and 4K worlds into the narrow pipelines of the internet.

Having distilled our message into dense, unpredictable chaos, it must now leave the safety of the source and traverse the harsh physical reality. We enter the domain of the Communication Channel. Assuming our perfectly compressed data is now an Independent Source, a stream of pure, uncorrelated information bits, which is hurled into an environment plagued by entropy’s chaotic twin: Noise. To mathematically model this hostility, we categorize the battlegrounds. The simplest are Memoryless Channels, where noise strikes each bit independently, entirely amnesiac to the past. This includes the elegant Binary Symmetric Channel (BSC), where the probability of a 0 flipping to a 1 is identical to a 1 flipping to a 0, and the asymmetric Z-channel, where a photon might be lost causing a 1 to become a 0, but darkness never spontaneously creates light. However, traversing a modern wireless network is rarely so polite. We must confront Channels with Memory, where interference is a violent, correlated storm. In a Block Fading Channel, a moving device passing behind a concrete building doesn’t just flip a single bit; it drowns out entire consecutive blocks of data. Faced with these diverse physical gauntlets, how do we evaluate a channel’s true potential? The ultimate metric, Channel Capacity ($C$), is defined as the maximum possible Mutual Information between the input and the output, which calculates the absolute mathematical “width” of the informational pipeline. It reveals the fundamental limit of truth that can survive the journey, regardless of the physical medium.

Having stripped our message of all natural redundancy, we have forged a fragile crystal of pure entropy. A single flipped bit in the chaotic channel could shatter its entire meaning. To survive this violent gauntlet, we must execute a paradoxical reversal, injecting mathematical armor, i.e. Channel Coding. For the random, isolated strikes of a Memoryless Channel, we weave algebraic dependencies between bits. By mapping our data into a higher-dimensional space, ensuring valid codewords are separated by a strict mathematical distance, we allow the receiver to detect and correct stray errors. But what of the devastating, continuous outages in Channels with Memory? A deep fade would obliterate any localized armor. Here, we employ Interleaving. By shuffling our coded bits across time before transmission and de-shuffling them upon arrival, we shatter concentrated bursts of destruction into scattered, manageable anomalies. However, can we ever achieve perfect, error-free communication in a fundamentally noisy universe? Intuition dictated that absolute certainty required infinite repetition, slowing transmission to a crawl. Shannon’s Second Theorem (The Noisy-Channel Coding Theorem) mathematically guarantees that as long as our transmission rate remains beneath the Channel Capacity ($C$), there exists an encoding strategy capable of achieving an error probability approaching exactly zero. It is the ultimate triumph of order over chaos, proving that truth can cross the most turbulent oceans of noise, completely unscathed.

Throughout this profound journey, we have reveled in the pristine logic of discrete bits. But the physical universe is inherently continuous. To apply our digital triumphs to these Analog Sources and transmit them across continuous Analog Channels, we must construct one final bridge. Because a machine cannot grasp infinite precision, we must force the continuous amplitude into discrete steps through Quantization. This violent rounding inherently introduces quantization noise, a fundamental distortion we must accept, yet one that is perfectly governed by the Rate-Distortion theory we explored earlier. But when these digitized bits are finally modulated back onto continuous electromagnetic waves to cross the physical ether, what governs their fate? The Shannon-Hartley Theorem ($C = B \log_2(1 + S/N)$), elegantly fuses the raw constraints of physics—the Bandwidth ($B$) of the medium and the Signal-to-Noise Ratio ($S/N$), to define the absolute capacity of a continuous channel. With this equation, we have captured the infinite continuous reality, distilled it into discrete entropy, armored it with algebraic logic, and hurled it flawlessly across the turbulent cosmos. The mathematical architecture of communication is now fully erected.

End - Information theory

Programming

C

C语言漫游

随着计算机迈入新纪元，高级语言如雨后春笋般涌现，其特性日新月异。正是在这样的时代背景下，C语言（C-Language）应运而生。

C语言以其面向过程的编程范式和与底层硬件的高度结合而著称。其构成元素（Elements of C）——包括简洁的关键字、灵活的标识符、多样的常量以及丰富的运算符等基本词法单元（Tokens），这些在当时堪称划时代的设计，深刻影响了后续众多编程语言。

作为一门面向过程的语言，C语言通过其强大的程序结构（Program structure），成功地将汇编语言中繁琐的底层细节抽象为清晰、富有逻辑性的操作，极大地提升了高级语言编程的效能与便捷性。C预处理器（Preprocessor） 首先通过 #include 指令引入头文件（通常包含函数声明和宏定义）、通过 #define 定义常量和宏等，在正式编译前对源代码进行初步处理，为后续的编译和链接奠定基础。而从更宏观的程序员视角来看，程序结构始于文件和整个程序的组织，不同源文件依据特定规则链接成可执行程序。深入其中，主函数（main function） 无疑是核心，其作为程序执行入口的特性便体现在其命名之中。然而，复杂的程序结构也带来了关于标识符生存周期（Lifetime）、作用域（Scope）、可见性（Visibility）以及链接属性（Linkage）等问题。编译器在处理这些问题时扮演了重要角色，它依赖于C语言精细的作用域规则和链接属性来管理标识符，避免命名冲突，这可以被视为一种基础的‘名字隔离’机制。

掌握了C语言的关键脉络后，便可以着手编写代码了。在实践中，我们首先会遇到声明（Declaration）与类型（Declarations and types）的问题：如何声明变量和函数？各种数据类型（Data Types）有何差异，应如何选用？变量、函数和类型的声明与初始化是这一环节的核心。C语言允许你通过 struct、union、enum 来定义用户定义数据类型（User-defined types），或使用 typedef 为复杂类型创建易读的别名。这些数据类型中，C语言的指针（Pointers） 占据着至关重要的地位，赋予了程序员直接访问和操作内存地址的能力，这也使得C程序员需要关注内存的精细管理，例如通过标准库函数进行动态内存分配与释放。同时，指针类型、数组类型和函数类型本身也是从其他类型派生出来的强大工具。运用复杂的声明符（Declarators）和数据类型组合，可以实现强大的功能。当然，要真正深入，我们还需探究它们的底层细节：它们占用多少内存？在内存中如何存储？为何以及如何使用不完整的类型（Incomplete Types）及其声明？

构建表达式与进行赋值（Expressions and assignments），是编写任何C程序都无法回避的核心操作。或许我们已能熟练运用简单运算，但在处理复杂逻辑时，如何区分左值（Lvalue）与右值（Rvalue）表达式？什么是常量表达式（Constant Expressions），其意义何在？如何理解并规避表达式求值可能引发的副作用（Side Effects）？以及一个关键概念序列点（Sequence Points），它是什么，又如何影响代码行为？此外，各类运算符的精确使用、新手常会遇到的运算符优先级（Operator Precedence）问题、C语言有时会“悄悄”进行的令人困惑的隐式类型转换（Implicit Type Conversion），以及功能强大且必须掌握的显式类型转换（Type Casting），都是学习C语言过程中至关重要且必须攻克的概念。

然后，深入到语句（Statements (C)）层面。作为一门面向过程的语言，语句是控制程序执行流（Execution Flow）的核心，也是我们需要重点掌握的内容。通过逐步学习并熟练运用C语言提供的各类语句，如选择语句、循环语句、跳转语句等及其结构与细节，我们将能够构建出逻辑严谨、功能强大的程序。

随着编程复杂度的提升，我们会倾向于将特定功能的代码块抽象为函数（Functions (C)）。函数是C语言中实现代码模块化、提升逻辑清晰度和简洁性的强大武器。作为基本的代码单元，函数本身也蕴含诸多细节：如内联函数（Inline Functions）的适用场景，存储类说明符（Storage Class Specifiers）对函数行为的影响，如何正确声明和使用返回类型（Return Type），以及实际参数（Arguments）与形式参数（Parameters）之间是如何传递与交互的。这些都是学习函数时不可忽视的要点。

在掌握了上述核心概念之后，C语言语法摘要（C language syntax summary）将是我们查漏补缺、巩固知识的环节。这里会涵盖C语言特定功能的完整说明、其语法表示法（Notation）的解读，以及如何精确确定任意语言组件的语法规则，帮助我们快速回顾和夯实基础。

当我们的C语言学习之旅暂告一段落时，会发现一个更为深入、颇具挑战性但也常被开发者津津乐道的领域——实现定义的行为（Implementation-defined behavior）。它直接关联到C语言著名的“可移植性问题（Portability Issues）”（例如，某些教材中讨论的像i+++++i这样臭名昭著的表达式，其行为就与编译器的具体实现紧密相关，是探讨可移植性时常会遇到的例子）。我们不会深入探讨此主题，有兴趣的读者可以参阅相关标准文档和编译器手册。我们在此仅作提醒：对于有志于攻克这类复杂问题的学习者，务必关注所用编译器的具体实现差异，以便查阅最相关的文档，勇敢地去探索这片深奥的水域吧！

End - C-Language

Java

Waiting for update…

Program design & Programming paradigms

Waiting for update…

Computer networking

Waiting for update…

Computer system programming

Waiting for update…

Software engineering

Waiting for update…

Theory-Oriented

Algebra

Waiting for update…

Analysis

Waiting for update…

Geometry

Not yet learned…

Waiting for update…

Stochastic processes

Not yet learned…

Waiting for update…

Mathematical Statistics

Not yet learned…

Waiting for update…